1. Heat equation
1.1. Introduction
The heat equation corresponding to no sources and constant thermal properties is given as

Equation (1) describes how heat energy spreads out. Other physical quantities besides temperature smooth out in much the same manner, satisfying the same partial differential equation (1). For this reason, (1) is also called the diffusion equation.
Since the heat equation in (1) has one time derivative, we must be given one initial condition (IC) (usually at t = 0), the initial temperature. It is possible that the initial temperature is not constant, but depends on x. Thus, we must be given the initial temperature distribution,

We also need to know that happens at the two boundaries, 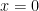 and
and  . Without knowing this information, we cannot predict the future. Two conditions are needed corresponding to the second spatial derivatives present in (1), usually one condition at each end. We call them boundary conditions. We deal with mainly four types of boundary conditions: Dirichlet, Neumann, Robin, and Periodic.
. Without knowing this information, we cannot predict the future. Two conditions are needed corresponding to the second spatial derivatives present in (1), usually one condition at each end. We call them boundary conditions. We deal with mainly four types of boundary conditions: Dirichlet, Neumann, Robin, and Periodic.
1.2. Separation of Variables (SoV)
When the PDE and the BCs are linear and homogeneous, we use a technique called the method of separation of variables to find the analytic solutions.
We introduce the heat operator,

The heat operator is a linear operator that satisfies the linearity property  .
.
A linear equation for the unknown  is of the form
is of the form

where 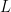 is a linear operator and
is a linear operator and  is known. The heat equation is a linear PDE:
is known. The heat equation is a linear PDE:

 is a forcing term. If
is a forcing term. If 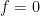 , then
, then  and the PDE becomes
and the PDE becomes

Equation (6) is a linear homogeneous equation.
We now propose to study heat equation with zero temperatures at finite ends:




defined for  and
and  . This problem consists of linear homogeneous partial differential equations with linear homogeneous boundary conditions.
. This problem consists of linear homogeneous partial differential equations with linear homogeneous boundary conditions.
Solution. We attempt to determine the product solution in the form of

First, we substitute equation (11) into equation (7),

We can “separate variables” by divide both sides of equation (12) by  :
:

Now the variables are “separated” in a sense that the left hand side is only a function of  and the right hand side is only a function of
and the right hand side is only a function of  . Next, we can claim that both sides of (13) must equal the same constant:
. Next, we can claim that both sides of (13) must equal the same constant:

where 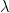 is a constant known as the separation constant.
is a constant known as the separation constant.
Equation (14) yields 2 ordinary differential equations,

and

We now see that the advantage of the product method is that it transform a PDE, which we do not have to solve, into two ODEs. The boundary conditions impose two conditions on the  -dependent ODE. The time-dependent ODE, equation (15), has no additional conditions. We can find a general solution for equation (15) quite easily,
-dependent ODE. The time-dependent ODE, equation (15), has no additional conditions. We can find a general solution for equation (15) quite easily,

where  is an arbitrary multiplicative constant. There can be three cases for
is an arbitrary multiplicative constant. There can be three cases for 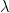 :
: 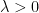 ,
, 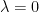 ,
,  . We will determine all allowable values of
. We will determine all allowable values of 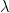 next.
next.
The ODE in (16) has two boundary conditions:


We call this a boundary value problem for ordinary differential equations. We note that  satisfy the ODE (16) and both BCs (18) and (19) regardless of the value of the separation constant. Thus,
satisfy the ODE (16) and both BCs (18) and (19) regardless of the value of the separation constant. Thus,  is a trivial solution of our PDE. It corresponds to
is a trivial solution of our PDE. It corresponds to  since
since  . However, we want to see if there are other nontrivial solutions. We will show that there are certain values of
. However, we want to see if there are other nontrivial solutions. We will show that there are certain values of 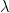 , called eigenvalues of the boundary value problem, for which there are nontrivial solutions,
, called eigenvalues of the boundary value problem, for which there are nontrivial solutions, 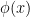 . The non-trivial solutions are called eigenfunctions corresponding to the eigenvalues
. The non-trivial solutions are called eigenfunctions corresponding to the eigenvalues 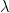
Now we solve equation (16). For linear and homogeneous second-order ODE, two independent solutions are usually obtained in the form of  . Substituting this result into equation (16) yields
. Substituting this result into equation (16) yields

and this implies that

We consider the three cases of 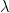 separately.
separately.
If  , the roots of the characteristic polynomials are
, the roots of the characteristic polynomials are  , so the solutions are
, so the solutions are  and
and  . The general solution is
. The general solution is

We use the hyperbolic functions,

We consider the BC from (18). Since  ,
, 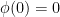 implies that
implies that  . So we have
. So we have  . Now we consider
. Now we consider  , which implies that
, which implies that  . Since
. Since  ,
,  . It follows that
. It follows that  . This implies that
. This implies that  . The only solution of (16) for
. The only solution of (16) for  that solves the homogeneous boundary condition is the trivial solution. Thus there are no negative eigenvalues.
that solves the homogeneous boundary condition is the trivial solution. Thus there are no negative eigenvalues.
We now consider the case of 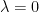 . The general solution is
. The general solution is

Apply 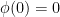 and we arrive at
and we arrive at 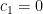 . Apply
. Apply  , we have
, we have  which implies that
which implies that  . This implies that
. This implies that  . The only solution of (16) for
. The only solution of (16) for 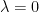 that solves the homogeneous boundary condition is the trivial solution. Thus
that solves the homogeneous boundary condition is the trivial solution. Thus 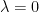 is not an eigenvalue for this problem.
is not an eigenvalue for this problem.
We now consider the case of 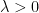 . The roots of the characteristic polynomials are
. The roots of the characteristic polynomials are  , so the solutions are
, so the solutions are  and
and  . The general solution is
. The general solution is

Since  and
and  are each linear combinations of
are each linear combinations of  and
and  , the general solution can also be expresed in the form of
, the general solution can also be expresed in the form of

For the BC 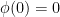 , we have
, we have  which implies that
which implies that  . Consider the BC
. Consider the BC  , we have
, we have  . If we let
. If we let  , then we arrive at
, then we arrive at  , a trivial solution. To find the nontrivial solutions, the eigenvalue
, a trivial solution. To find the nontrivial solutions, the eigenvalue 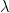 much satisfy
much satisfy

 must be the zero of the sine function. Thus,
must be the zero of the sine function. Thus,

The eigenvalues are

The eigenfunctions corresponding to the eigenvalues are

Now we know that the product solution consists of  and
and  where we determined from the boundary conditions
where we determined from the boundary conditions 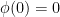 and
and  . We call this type of boundary conditions the Dirichlet boundary conditions. Thus, the product solutions of the heat equation with homogeneous Dirichlet boundary conditions are
. We call this type of boundary conditions the Dirichlet boundary conditions. Thus, the product solutions of the heat equation with homogeneous Dirichlet boundary conditions are

where B is an arbitrary constant.
1.3. Initial value problems
The principle of superposition can be extended to show that if  are solutions of a linear homogeneous problem, then any linear combination of these is also a solution,
are solutions of a linear homogeneous problem, then any linear combination of these is also a solution,  ,where
,where 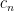 are arbitrary constants. Since we know from the method of separation of variables that
are arbitrary constants. Since we know from the method of separation of variables that  is a solution of the heat equation (solving zero boundary conditions) for all positive
is a solution of the heat equation (solving zero boundary conditions) for all positive  , it follows that any linear combination of these solutions is also a solution of the linear homogeneous heat equation. Thus,
, it follows that any linear combination of these solutions is also a solution of the linear homogeneous heat equation. Thus,

For example, we wish to solve the following initial value problem:




Solution. We can let  and
and  such that
such that  . We can use the product solutions from (31) and we see that the product solution satisfy the initial conditions
. We can use the product solutions from (31) and we see that the product solution satisfy the initial conditions  . By picking
. By picking  and
and 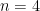 , we have satisfied the initial condition
, we have satisfied the initial condition  . The solution we get is
. The solution we get is

By picking  and
and  , we have satisfied the initial condition
, we have satisfied the initial condition  . The solution we get is
. The solution we get is

By superposition principle we know that the product solution of our problem is a linear combinations of  and
and  . Thus,
. Thus,


The IC in the previous problem is a finite sum of the sine functions. What should we do in the situation that the IC is not a finite linear combinations of the sine functions? Consider the following problem:




Solution. From equation (32) we know that the solution is

We want to apply the IC to our problem. First, from the previous problem, note that we can solve the heat equation if initially

Thus, we use the theory of Fourier series and claim that “any” (with restrictions) initial condition 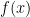 can be written as an infinite linear combination of
can be written as an infinite linear combination of  , known as a type of Fourier series:
, known as a type of Fourier series:

We want to determine the coefficient  in equation (46). To do that, we use the fact the
in equation (46). To do that, we use the fact the  satisfies the following orthogonality relation:
satisfies the following orthogonality relation:

Multiply (46) by  and integrating from
and integrating from  to
to 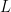 yields
yields

Solving for 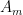 yields,
yields,

Now, we calculate the coefficient  from equation (49) for
from equation (49) for  ,
,

Solving for  yields,
yields,

Each succeeding term in the series is much smaller than the first. We can then approximate the infinite series by only the first term:


Let us summarize the method of separation of variables as it appears for the heat equation with homogeneous Dirichlet boundary conditions:




- Make sure that you have a linear and homogeneous PDE with linear and homogeneous BC.
- Temporarily ignore the nonzero IC.
- Separate variables (determine differential equations implied by the assumption of product solutions) and introduce a separation constant.
- Determine separation constants as the eigenvalues of a boundary value problem.
- Solve other differential equations. Record all product solutions of the PDE obtainable by this method.
- Apply the principle of superposition (for a linear combination of all product solutions).
- Attempt to satisfy the initial condition.
- Determine coefficients using the orthogonality of the eigenfunctions.
1.4. Other Boundary Value Problems
The following problem is defined for  and
and  .
.




This is a heat conduction problem in a one-dimensional rod with constant thermal properties and no sources. The ends of the rod are insulated. Both the PDE and BCs are linear and homogeneous. We call this type of BC the Neumann boundary condition. We apply SoV.
Solution. The assumed product solutions are:

Substitute into the PDE,

where 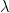 is the separation constant. This implies that
is the separation constant. This implies that


Solving (64),

The insulated BCs imply that the separated solutions must satisfy


We determine the separation constant 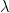 by finding those
by finding those 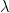 for which nontrivial solutions exist.
for which nontrivial solutions exist.
For  , the general solution is
, the general solution is

We also need

The BC  implies that
implies that  , and
, and  means that
means that

Since  ,
,  . This implies that
. This implies that 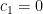 . Since
. Since  is a trivial solution, there is no negative eigenvalues.
is a trivial solution, there is no negative eigenvalues.
For 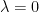 , the solution is
, the solution is

and

Both BCs give  . Thus, there are non trivial solutions of the BVP for
. Thus, there are non trivial solutions of the BVP for 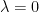 , namely,
, namely,

The time dependent part gives  . Thus, the resulting product solution of the PDE is
. Thus, the resulting product solution of the PDE is

where  is any constant.
is any constant.
For 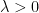 , the solutions is in the form
, the solutions is in the form

which gives

and

The BC  implies that
implies that  , so
, so  . The BC
. The BC  gives
gives

For nontrivial solutions,  . This gives us
. This gives us  .
.

However, the corresponding eigenfunctions are cosines,

The product solution of the PDE is

where A is a arbitrary multiplicative constant.
In order to satisfy the IC, we use the principle of superposition so that,

The IE  is satisfied if
is satisfied if

for  .
.
To complete the solution, we need to determine the arbitrary coefficient 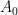 and
and 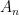 . We use the fact that
. We use the fact that  satisfies the following orthogonality relation:
satisfies the following orthogonality relation:

for  and
and 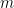 nonnegative integers.
nonnegative integers.
Multiply (83) by  and integrating from
and integrating from  to
to 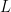 yields
yields

Solving for 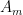 yields,
yields,



that is defined for
is called periodic if there is a number
such that
. A periodic function has the following properties:
has period
, then
for all
and for all integers
.
has period
.
has period
, then
does not depend on
.
, its periodic extension is
. This definition does not specify what the periodic extension is at the endpoints
. In fact, the function
may have jump discontinuities at the endpoints if the the one-sided limits
and
both exist but not equal.
is symmetric with respect to the y axis.
is symmetric with respect to the origin.
is an even function if
is even and is an odd function if n is odd. The functions cos
, cosh
, and any function of
are even functions. The functions sin
, tan
, and sinh
are odd functions. In fact, the products of functions follow the usual rules: even × even = even, odd × odd = even, odd × even = odd. The sum of two odd functions is again odd, and the sum of two evens is even.
be any function at all defined on
. Let
and
. Then we easily check that
, that
is even and that
is odd. The functions
and
are called the even and odd parts of
, respectively. If
is any polynomial, its even part is the sum of its even terms, and its odd part is the sum of its odd terms.
is even, then both
and
are odd. If
is odd, then its derivative and integral are even.
must pass through the origin since
follows directly from (4) by putting
. The graph of an even function
must cross the
axis horizontally,
, since the derivative is odd (provided the derivative exists).
: Dirichlet BCs corresponding to the odd extension
: Nuemann BCs corresponding to the even extension
: Periodic BCs corresponding to the periodic extension





